Introduction to Score-based Generative Models

Generative Model는 현실에 존재할만한 그럴듯한(High-fidelity) 이미지를 만들거나, Semi-supervised Learning, Few-Shot Learning 등의 문제에서 성능을 향상시키거나, 적대적 예제나 이상치 탐지를 하는 데 이용하는 등 다양한 응용 문제들에 활용될 수 있습니다. 대표적인 예로 흔히들 잘 알려져 있는 Autoencoder, VAE, GAN, Normalizing Flows를 들 수 있을 것입니다.
이번 글에서는 이와는 다른 방법론인 Score-based Generative Modeling에 대해서 다뤄보도록 하겠습니다.
이 글에서 주로 다룰 논문은 아래와 같습니다.
Generative Modeling by Estimating Gradients of the Data Distribution, NeurIPS 2019 (Oral)
Score-Based Generative Modeling through Stochastic Differential Equations, ICLR 2021 (Oral)
Generative Modeling의 대표적 접근 방법과 한계점

Generative Modeling의 대표적인 방법은 크게 Autoencoder, VAE, Normalizing Flows와 같은 Likelihood-based 방법과 샘플을 생성해내는 Generator와 생성된 샘플과 실제 샘플을 분류하는 Discriminator를 적대적으로 학습시키는 Generative Adversarial Networks(GAN) 방법이 있습니다.
하지만 위의 두 방법들은 각각 다른 단점을 갖고 있습니다.
Likelihood-based 방법은 Normalized Probality Model을 구성해야 하기 때문에 특정한 종류의 아키텍처를 써야하거나(Autogressive Model, Flow Model), VAE의 경우 생성해낸 확률 분포에 대해 직접 Loss를 계산하는 것이 아닌 ELBO와 같은 대체 Loss(Surrogate Loss)를 사용해 학습을 해야 합니다.
GAN 방법은 위와 같은 Likelihood-based 방법의 한계점들을 피해나갈 수 있지만 학습 과정이 다소 불안정하며, GAN의 Adversarial Loss의 특성으로 인해 서로 다른 GAN 모델을 비교하고 평가하는데 부적합하다는 단점이 있습니다.
Generative Modeling by Estimating Gradients of the Data Distribution
Score
이에 Yang Song은 NeurIPS 2019년도에 데이터의 Log likelihood인 Score를 이용한 Generative Modeling 방법론을 제안합니다. Score는 아래와 같이 간단하게 표현할 수 있습니다.
$$\nabla_\mathbf{x} \log{p(\mathbf{x})}$$
Score는 Gradient의 의미 그대로, log data density가 가장 커지는 방향을 표현하는 벡터라고 생각할 수 있습니다.
이는 Stochastic Gradient Descent에서 Loss를 감소시키는 Model Parameter의 Gradient 벡터를 $-\nabla_{\theta} \log(\mathcal{L}(\theta))$로 표현한다는 것과 연결지어 이해해볼 수 있습니다. 다만 여기서 우리의 목표는 Data Sampling이기 때문에 Model Parameter에 대한 Score가 아닌 Data Density에 대한 Score를 이용한다는 점을 주의해야 합니다.
Score Matching
하지만 대부분의 머신 러닝의 문제에서 그렇듯, 데이터 전체 분포에 대한 Score를 계산하는 것은 불가능하기 때문에 우리는 이러한 Score를 추정하는 Score Estimator를 학습해야 합니다. 이렇게 임의의 데이터의 Score를 추정하는 Score Estimator $ \mathbf{s}_\theta(x) $ 를 학습하는 방법을 Score Matching이라고 부릅니다. Score Matching의 Objective를 수식으로 나타내면 아래와 같이 Score Estimator가 추정한 Score와 실제 Score 간의 Mean Squared Error로 표현할 수 있습니다.
$$ \mathcal{L}_\theta = \frac{1}{2} \mathbb{E}_{p_{data}} {\Vert \mathbf{s_{\theta}(x)} - \nabla_\mathbf{x} \log{p_{data}(\mathbf{x})} \Vert}^2_2 $$
이때 $ p_\text{data}(\mathbf{x}) $ 는 특정한 Sample이 갖는 Density 자체를 나타내기 때문에 직접적으로 계산하는 게 불가능합니다. 이러한 까닭에 위 식을 Score Matching을 제안한 논문 [1]의 증명에 의해 $ p_\text{data}(\mathbf{x}) $ 에 의존하지 않는 형태로 아래와 같이 유도할 수 있습니다.
$$ \mathbb{E}_{p_{data}(\mathbf{x})} \bigg[ \operatorname{tr} (\nabla_{\mathbf{x}} \mathbf{s_{\theta}(x)}) + \frac{1}{2} \lVert \mathbf{s_{\theta}(x)} \rVert^2_2 \bigg] $$
특정한 Regularity condition 하에 위의 Loss를 이용해 실제 Score를 추정하는 Optimal Score Estimator를 학습하는 게 가능하단 게 밝혀진 바 있지만, 문제는 $ \mathbf{s_\theta(x)} $의 Jacobian인 $ \nabla_{\mathbf{x}} \mathbf{s_\theta(x)} $의 계산으로 인해 Deep Networks나 고차원의 데이터까지 확장할 수 없다는 문제점이 있습니다.
Denoised Score Matching
이를 해결하기 위해 제안된 대표적인 방법으로 Denoising Score Matching [2]이 있습니다.
Denoising Score Matching은 $ \text{tr}( \nabla_\mathbf{x} \mathbf{s_\theta(x)} ) $ 를 완전히 피하기 위한 방법으로, 원본 데이터에 대한 Score를 계산하는 대신 미리 정의된 노이즈 분포 $ q_\sigma (\tilde{\mathbf{x}} | \mathbf{x}) $ 를 이용해 Pertubed data distribution $ q_\sigma(\tilde{\mathbf{x}}) \triangleq \int q_\sigma (\tilde{\mathbf{x}} | \mathbf{x})p_{data}(\mathbf{x})\mathrm{d}\mathbf{x} $ 에 대한 Score Matching을 진행합니다.
이를 종합하면 아래와 같은 Loss가 됩니다.
$$ \mathcal{L}_\theta = \frac{1}{2}\mathbb{E}_{q_\sigma (\tilde{\mathbf{x}} | \mathbf{x})p_{data}} [ \Vert\mathbf{s}_\theta(\tilde{\mathbf{x}}) -\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \Vert^2_2] $$
전체적으로 기존 Score Matching의 Loss에서 원본 데이터 분포에 대한 항을 Pertubed Data Distribution에 대한 항으로 변경한 수식이라고 이해할 수 있습니다. 데이터 분포에 대한 Density를 직접적으로 계산하는 건 불가능하지만 우리가 사전에 정의한 Pertubed Data Distribution의 Density를 측정하는 것은 가능합니다. 이와 같이 전체 데이터 분포에 대한 계산을 Pertubed Data Distribution에 대한 계산으로 우회함으로써 Denoised Score Matching은 보다 현실적인 데이터 스케일에서 작동할 수 있습니다.
Sampling with Langevin Dynamics
Score Matching은 위에서 말했듯이, Log Data density의 Gradient를 추정하는 모델을 학습하는 방법에 불과합니다. 그렇다면 일반적인 Generative Model이 그렇듯이 새로운 이미지를 하나 생성하고 싶다면 어떻게 해야 할까요?
아이디어는 간단합니다. 일반적으로 SGD를 이용해 Weight를 업데이트할 때 $ \theta_t = \theta_{t-1} - \eta \nabla_\theta \mathcal{L}(x ; \theta) $ 와 같이 특정 Weight에서 Weight에 대한 Gradient를 빼는 방식으로 Loss를 줄이는 Weight를 찾았습니다. 이와 비슷하게 좀 더 그럴듯한 Data를 만들고 싶다면 특정 Data에 Data에 대한 Gradient를 더해주는 방식으로 Likelihood가 높아진 (좀 더 그럴듯한) Data를 찾을 수 있을 것입니다. 이를 염두에 두고 Sampling with Langevin Dynamics를 나타내는 수식을 살펴보겠습니다.
$$ \tilde{\mathbf{x}}_t =\tilde{\mathbf{x}}_{t-1} + \frac{\epsilon}{2} \nabla_{\mathbf{x}} \log{p(\tilde{\mathbf{x}}_{t-1}}) + \sqrt{\epsilon} \mathbf{z}_t, \quad \text{where } \mathbf{z}_t \sim \mathcal{N}(0, I) $$
여기서 $ \mathbf{z}_t $ 에 대한 항은 데이터를 업데이트할 때 랜덤성(Noise)을 부여합니다. 처음에 노이즈 샘플로부터 시작해 Score와 랜덤 노이즈를 매 스텝마다 부여하는 과정을 반복함으로써 데이터를 업데이트합니다. 위의 수식을 통해 최종적으로 ($ \epsilon \rightarrow 0 $, $ T \rightarrow \infty $) 얻는 샘플 $ \tilde{\mathbf{x}}_T $의 분포는 특정한 regularity 조건 하에 원래 데이터 분포인 $ p(\mathbf{x}) $와 동일합니다[3]. 이와 같은 방법으로 Score를 이용해 원래 데이터 분포에서의 샘플링을 수행할 수 있습니다. 이때 우리는 위에서 Score Mathcing을 통해서 $ \nabla_{\mathbf{x}} \log{p(\tilde{\mathbf{x}}_{t-1}}) $를 추정하는 Score Network $\mathbf{s}_\theta(\mathbf{x}) $ 를 설명한 바 있습니다.
이렇게 Score Matching과 Sampling with Langevin dynamics를 결합한 방법을 Denoising Score Matching with Langevin Dynamics (SMLD) 라고 부릅니다.
일반적으로 이러한 SMLD을 조금 더 발전시켜, 데이터를 다양한 레벨의 노이즈로 변환하고, 변환된 각 데이터의 Score를 하나의 Conditional Score Network $ \mathbf{s}_\theta(\mathbf{x}, \sigma) \approx \nabla_\mathbf{x} \log q_\sigma(\mathbf{x}) $ 를 이용하여 추정하는 Noise Conditional Score Network 를 이용합니다.
Denoising Diffusion Probabilistic Modeling
SMLD와 같은 방법론은 노이즈를 점점 증가시켜 가면서 학습 데이터를 특정한 Noise Distribution으로 변환한 후, 다시 이러한 Noise Distribution으로부터 학습 데이터를 복원하는 방법이라고 설명할 수 있습니다.
Denoising Diffusion Probabilistic Modeling (DDPM) [4] 또한 원본 데이터 분포를 노이즈 분포로 변환한 후, 다시 이 노이즈 분포를 원본 데이터 분포로 변환한다는 점에서는 유사하지만, 전체 변환 과정을 명시적인 확률 모델로 이루어진 Discrete Markov Chain으로 표현한다는 점에서 차이가 있습니다.
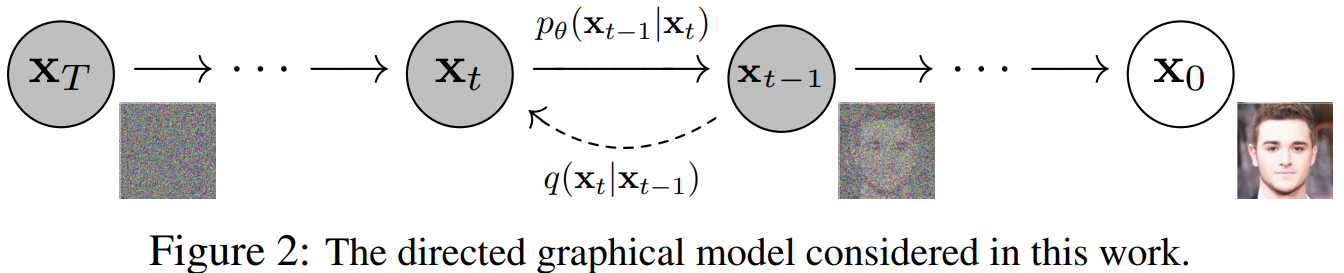
데이터를 노이즈 분포로 변환하는 하나의 스텝을 Gaussian Distribution으로 표현한다면 아래와 같이 표현될 수 있습니다.
$$ p(\mathbf{x}_i | \mathbf{x}_{i-1}) = \mathcal{N}(\mathbf{x}_i ; \sqrt{1-\beta_i} \mathbf{x}_{x-i}, \beta_i \mathbf{I}) $$
이를 고려해 처음 데이터로부터 i번째 변환한 분포를 다시 아래와 같이 표현할 수 있습니다.
$$ p_{\alpha_i} (\mathbf{x}_i | \mathbf{x}_0 ) = \mathcal{N} (\mathbf{x}_i ; \sqrt{\alpha_i} \mathbf{x}_0, (1 - \alpha_i) \mathbf{I}), \quad \text{where } \alpha_i \triangleq \prod_{j=1}^i (1 - \beta_j) $$
forward transformation을 Gaussian Distribution 형태로 표현했기 때문에, 반대로 노이즈 분포로부터 원본 데이터로 변환하는 하나의 스텝 또한 아래와 같이 Gaussian Distribution 형태로 표현할 수 있을 것입니다.
$$ p_\theta(\mathbf{x}_{i-1}|\mathbf{x}_i) = \mathcal{N}(\mathbf{x}_{i-1} ; \frac{1}{\sqrt{1-\beta_i}} ( \mathbf{x}_i + \beta_i \mathbf{s}_\theta ( \mathbf{x}_i, i)), \beta_i, \mathbf{I}) $$
이미지를 생성할 때는 최종 노이즈 데이터 $ \mathbf{x}_N \sim \mathcal{N}(\mathbf{0, I}) $ 로부터 시작해서 아래와 같은 스텝을 N번 거쳐 샘플링할 수 있습니다.
$$ \mathbf{x}_{i-1} = \frac{1}{\sqrt{1-\beta_i}} ( \mathbf{x}_i + \beta_i \mathbf{s}_{\theta^\ast} (\mathbf{x}_i, i)) + \sqrt{\beta_i} \mathbf{z}_i, \quad i = N, N - 1, \dots, 1. $$
이와 같이 미리 정의한 조건부 확률 분포로 구성된 $\prod_{i=1}^N p_\theta (\mathbf{x}_{i-1}|\mathbf{x}_i) $으로부터 이미지를 샘플링하는 방법을 Ancestral Sampling이라고 부릅니다. 추후에 이 Ancestral Sampling을 발전시킨 방법을 다룹니다.
DDPM 또한 데이터의 Score를 간접적으로 추정한다는 면에서, SGLD와 DDPM 모두 Score-based Generative Model이라고 부를 수 있습니다.
Score-based Generative Modeling through Stochastic Differential Equations (SDEs)
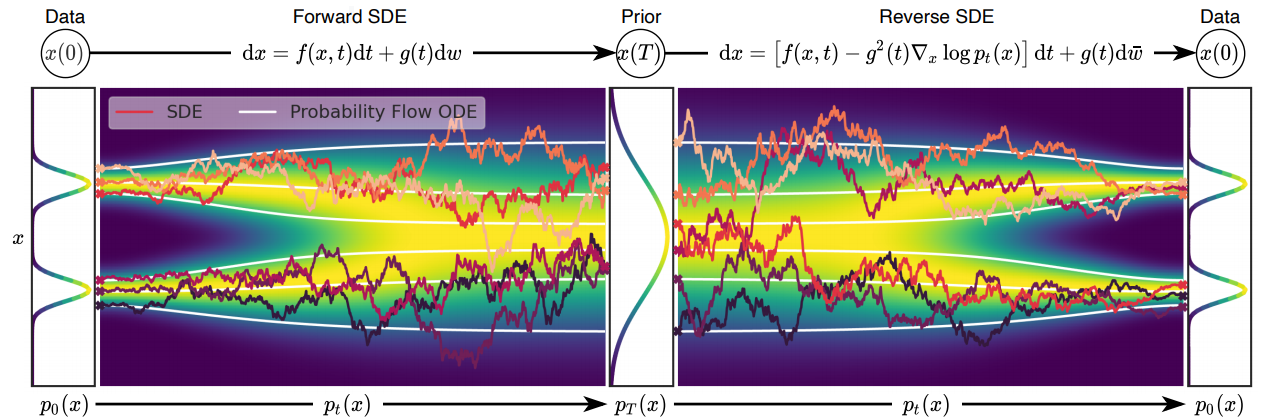
두 방법론의 핵심은 여러 노이즈 스케일에 따라 데이터를 노이즈로 변환하고, 다시 이 노이즈로부터 원본 데이터를 복원하는 과정입니다. 만약 이러한 노이즈 스케일이 한정되어 있지 않고 무한하다면 조금 더 정밀하게 이 과정을 진행할 수 있지 않을까요?
본 논문은 이러한 관점에서 Noise를 time variable로 취급하여 Stochastic Differential Equations (SDE) 관점에서 두 방법론을 통합하는 프레임워크를 제안합니다. 즉, 원본 데이터 분포에 Noise를 조금씩 첨가해 사전에 정의된 노이즈 분포 형태로 변환하는 SDE와, 이에 대응되는 Reverse-time SDE를 이용해 노이즈 분포로부터 Noise를 조금씩 제거해 원본 데이터 분포로 변환한다는 관점으로 두 방법론을 통합적으로 설명합니다.
Stochastic Differential Equation (SDE)
미분 방정식(Differential Equation)의 기본적인 목적 중 하나는, 원래 함수를 모를 때 도함수와 함수값을 이용해서 원래 함수를 추정하거나 현재 관측하지 않은 변수에서의 함수값을 추정하는 것입니다.
Stochastic Differential Equation은 Random Variable이 들어간 Stochastic Process가 포함된 미분 방정식입니다. 일반적으로 랜덤성 또는 노이즈가 포함된 주식 값의 변동이나, 열역학 운동을 표현할 때 주로 사용됩니다. 본 논문은 데이터를 노이즈의 Scale에 따라 변환하는 Diffusion Process를 time variable $ t $ 에 대한 Stochastic Process로 해석하는 방식으로 Score-based Generative Model의 방법론들을 SDE로 표현하였습니다.
Pertubing Data with SDEs
초기값을 $ \mathbf{x}(0) \sim p_0 $ 으로, 최종 변환된 데이터를 $ \mathbf{x}(T) \sim p_T $로 표현할 때 time variable $ t \in [0, T] $ 에 대해서의 데이터를 $ \{ \mathbf{x}(t)^T_{t=0} \} $ 으로 표현할 수 있습니다. 이때 $ p_0 $은 원본 데이터 분포이며, $ p_T $ 는 사전 분포입니다. 이때 time variable $ t $에 따라 데이터가 업데이트되는 Diffusion Process는 아래와 같이 SDE로 표현할 수 있습니다.
$$ \mathrm{d}\mathbf{x} = \mathbf{f}(\mathbf{x}, t)dt + g(t) \mathrm{d} \mathbf{w} $$
여기서 $ f(\cdot, t) : \mathbb{R}^d \rightarrow \mathbb{R}^d $는 $ x(t) $의 drifft coefficient 로 불리는 함수이며, $ g(\cdot) : \mathbb{R} \rightarrow \mathbb{R} $ 는 diffusion coefficient로 불리는 함수이며, $ \mathbf{w}$는 Standard Winer Process로 랜덤성을 표현하는 항입니다. 즉 $ f(\cdot, t) $은 $ \mathbf{x} $에 따른 함수값을 주로 나타내며, $ g(\cdot) $은 해당 함수값에 얼마큼의 Diffusion(Noise 또는 랜덤성)을 부여하는지 나타내는 항이라고 이해할 수 있습니다.
이러한 SDE는 state와 time 모두에서 coefficient가 전역적으로 립시츠 연속성을 만족할 때 유일하며 강한 해(Strong Solution)를 갖는 것으로 알려져 있습니다.
Generating Samples by Reversing the SDE
이미지를 생성할 때는 기존 방법론과 마찬가지로 노이즈 데이터 $ \mathbf{x}(T) \sim p_T $ 로부터 원래 과정의 역(reverse)을 통해 $ \mathbf{x}(0) \sim p_0 $ 를 샘플링할 수 있습니다. 특히 Diffusion Process의 역 또한 Diffusion Process로 reverse-time SDE는 다음과 같은 수식으로 나타낼 수 있습니다.
$$ \mathrm{d}\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g(t)^2 \nabla_x \log p_t(\mathbf{x})]dt + g(t) \mathrm{d} \bar{\mathbf{w}} $$
위의 수식을 통해 $ p_0 $ 으로부터 이미지를 생성하는 Reverse diffusion process를 유도해낼 수 있습니다.
Estimating Scores for the SDE
위 수식에서 score에 대한 항인 $ \nabla_\mathbf{x} \log p_t(\mathbf{x}) $ 를 확인할 수 있듯이, Noise Conditional Score Network를 연속적으로 일반화한 time-dependent score-based model $\mathbf{s}_\theta (\mathbf{x}, t) $ 를 학습해야 합니다. 해당 모델은 아래와 같이 얻어질 수 있습니다.
$$ \theta^\ast = \underset{\theta}{\text{arg min }} \mathbb{E}_t \Big\{ \lambda(t) \mathbb{E}_{\mathbf{x}(0)} \mathbb{E}_{\mathbf{x}(t)} \left[ \Vert \mathbf{s}_\theta(\mathbf{x}(t), t) - \nabla_{\mathbf{x}(t)} \log p_{0t} (\mathbf{x}(t) | \mathbf{x}(0)) \Vert^2_2 \right] \Big\} $$
여기서 $\lambda : [0, T] \rightarrow \mathbb{R}^+ $는 양수의 Weighting Function, $ t $는 $[0, T]$에서 Uniform Distribution에서 샘플링한 것이며, $\mathbf{x}(0) \sim p_0(\mathbf{x}) $와 $\mathbf{x}(t) \sim p_{0t}(\mathbf{x}(t) | \mathbf{x}(0)) $ 는 각각 해당 분포로부터 샘플링된 것입니다. 이때 $ p_{0t} (\mathbf{x}(t) | \mathbf{x}(0)) $ 는 초기값( $\mathbf{x}(0)$ )에서 t번째 값( $\mathbf{x}(t)$ )으로 이동하는(transition) 분포를 표현한 것입니다.
얼핏 보기에는 복잡해보이지만, 위의 수식은 사실 Denoised Score Matching에서 소개한 Loss를 Noise Conditional Score Network에 대한 표현( $\mathbf{s}_\theta(\tilde{\mathbf{x}}, \sigma_i)$ )으로 바꾸고, 다시 노이즈에 대한 변수( $\sigma_i$ )와 Pertubed Data Distribution $p_{\sigma_i}(\tilde{\mathbf{x}} | \mathbf{x})$ 을 각각 time variable $ t $와 $ p_{0t}(\mathbf{x}(t) | \mathbf{x}(0)) $로 바꾼 것에 불과합니다.
즉, Denoised Score Matching 방법과 마찬가지로 SDE 프레임워크에서 Score Network를 학습할 수 있음을 말하고 있으며, 이외의 구체적인 고려사항들은 해당 논문에서 확인할 수 있습니다.
SMLD and DDPM as SDE
맨 처음에 말했듯이, 본 논문의 목적은 기존 Score-based Generative Model인 SMLD와 DDPM을 SDE 관점으로 설명하는 것이었습니다. 두 방법은 SDE 기반 방법을 Discretization한 방법으로 이해할 수 있습니다.
핵심은 노이즈 분포 (또는 pertubation kerenl $p_{\sigma_i}(\mathbf{x}|\mathbf{x}_0)$ )를 discrete Markov chain으로 표현하고 이로부터 다시 reverse Markov chain을 구하는 것입니다.
SMLD에서는 각 스텝에서의 노이즈 분포를 $ q_{\sigma_i}(\tilde{\mathbf{x}} | \mathbf{x}) = \mathcal{N}(\tilde{\mathbf{x}} | \mathbf{x}, \sigma_i^2 I) $처럼 나타낼 수 있고 이를 다음과 같은 Markov Chain으로 표현할 수 있습니다.
$$ \mathbf{x}_i = \mathbf{x}_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} \mathbf{z}_{i-1}, \quad i = 1, \dots, N \text{, where } \mathbf{z}_{i-1} \sim \mathcal{N}(\mathbf{0, I})$$
DDPM의 pertubation kernel 또한 마찬가지로 다음과 같은 discrete Markov chain으로 표현할 수 있습니다.
$$ \mathbf{x}_i = \sqrt{1-\beta_i} \mathbf{x}_{i-1} + \sqrt{\beta_i} \mathbf{z}_{i-1}. \quad i = 1, \dots, N. $$
본 논문에서는 이러한 pertubation kernel에 의한 $\mathbf{x}(t)$를 SDE로 표현하고 이를 증명하는 것까지 소개되어 있지만, 이 글에서는 생략하도록 하겠습니다.
Solving the Reverse SDE
우리가 보다 초점을 맞춰야 할 부분은 Runge-Kutta methods와 같은 SDE를 풀기 위한 General-purpose Solver들이 잘 알려져 있고 reverse-time SDE를 통한 샘플 생성 또한 가능하다는 것입니다. DDPM의 Ancestral Sampling 또한 reverse-time SDE를 Discretization한 하나의 예일 뿐이고, 다른 방식의 discretization으로는 더 나은 성능을 확보할 수도 있을 것입니다.
본 논문에서는 forward SDE에서 사용된 것과 동일한 discretization을 reverse-time SDE에 적용한 Reverse Diffusion Sampler를 소개합니다. 구체적인 알고리즘은 다음 그림에서 확인할 수 있습니다. Algorithm1과 Algorithm2의 3~5번 줄에 해당하는 영역이 각각 SMLD와 DDPM의 Reverse Diffusion Sampler를 표현하고 있습니다.

또한 샘플링한 결과를 보정하기 위해 SMLD에서 사용되었던 Langevin Dynamics(위 그림에서 6~8번 줄)를 추가적으로 사용할 수 있을 것습니다. 이를 본 논문에서는 Corrector라 부르고, Predictor와 Corrector를 결합한 Predictor-Corrector (PC) sampler를 제안합니다.
이때 Algorithm 1에서 Predictor를 제거하고 Corrector만 사용하면 기존 SMLD와 같고, Algorithm 2에서 Corrector를 제거하고 Predictor만 사용하면 Ancestral Sampling을 Reverse Diffusion Sampler로 교체한 DDPM과 같습니다.
Experiments
제안한 PC sampler에 대한 실험 결과는 다음과 같습니다.

전체적으로 보았을 때 Langevin Dynamic Sampling을 이용하는 C2000이 DDPM의 Ancestral Sampling이나 본 논문에서 제안한 Reverse Diffusion Sampler보다 성능이 확연히 낮은 것을 확인할 수 있습니다. 하지만 본 논문에서 제안한 Reverse Diffusion Sampler와 Langevin Dynamic Sampling을 결합한 PC Sampler를 사용할 때 전체적으로 성능이 높은 것을 확인할 수 있습니다.
여기서 probability flow는 SDE를 이에 대응되는 ODE (Ordinary Differential Equation)로 표현한 Determinisic Process로 구성한 모델입니다. Stochasticity (랜덤성)을 제거했기 때문에 제안한 모델보다 더 적은 스텝으로도 Efficient Sampling이 가능하고, 정확한 likelihood 계산이 가능하다는 점을 장점으로 말하고 있습니다.
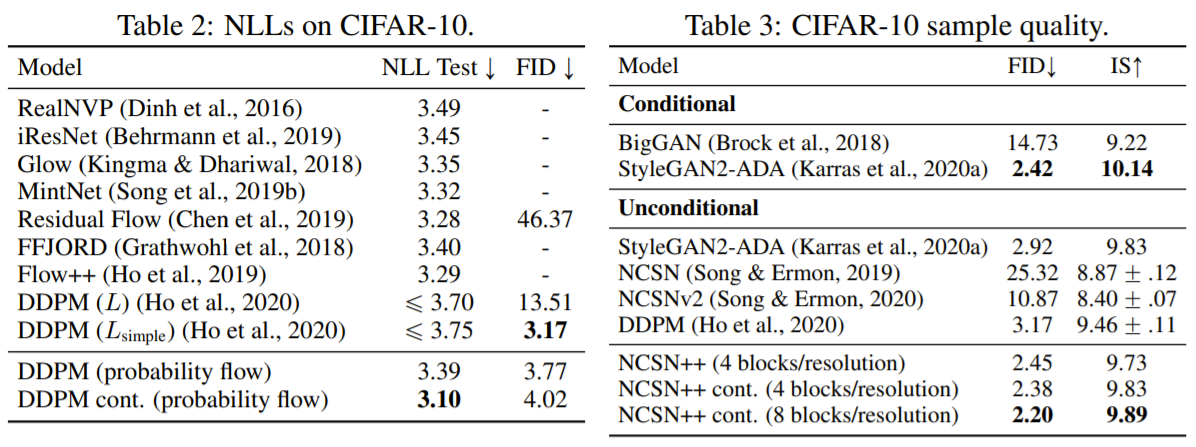
최종적으로 PC Sampler와 Probability Flow 및 간단한 개선 사항을 추가시킨 DDPM 기반 모델과 SMLD 기반 모델(NCSN)에 대한 실험 결과는 위와 같습니다. 특히 CIFAR-10에서 FID와 IS 모두 기존 모델과 비교했을 때 큰 성능 차로 SOTA 성능에 도달한 게 주목할 만합니다.
또한 Score-based Generative Model로서 최초로 1024x1024 크기의 high fidelity 이미지 생성이 가능하다는 점을 보이면서 Score-based Generative Model이 단순히 수학적인 명료함뿐만 아니라 실용적으로 사용될 수 있는 가능성도 충분히 가질 수 있음을 보여주고 있습니다.

Conditional Generation with an Unconditional Model
마지막으로 본 논문은 SDE Formulation을 이용해 단순히 이미지를 생성할 뿐만 아니라 특정 레이블에 해당하는 이미지를 생성하는 Conditional Sampling이 가능하다는데 흥미로운 지점 중 하나입니다. 수식을 보면 아래와 같습니다.
$$ \mathrm{d}\mathbf{x} = \{\mathbf{f}(\mathbf{x}, t) - g(t)^2 [ \nabla_\mathbf{x} \log p_t(\mathbf{x}) + \nabla_\mathbf{x} \log p_t ( \mathbf{y} | \mathbf{x}) ] \} \mathrm{d}t + g(t)\mathrm{d} \bar{\mathbf{w}} $$
여기서 주의 깊게 봐야 할 점은 기존 reverse-time SDE에서 단순히 time-dependent classifier $p_t(\mathbf{y} | \mathbf{x}(t)) $를 추가했다는 점입니다. 즉, 학습 단계에서 Generative Model과 동시에 Classifier를 같이 학습하고, 이를 conditional reverse-time SDE에 포함해 Sampling을 진행하면 조건부 샘플링이 가능하다고 설명하고 있습니다. (본 논문의 Appendix I 참고)

또한 단순히 class-conditional sampling뿐만 아니라 Inpainting이나 Colorization 또한 가능하다고 언급하면서, Score-based Generative Model이 굉장히 유연하게 다양한 Task에 대한 Conditional Generation이 가능하다는 것을 보여주고 있습니다.
Discussion
Score-based Generative Model은 수학적인 명료함을 가지면서도 학습이 불안한 GAN-based Model이나, 모델의 구조에 Constraint가 있는 Likelihood-based Model의 한계점에서 벗어난 Generative Model 방법론이라고 부를 수 있습니다.
하지만 Score-based Generative Model은 Sampling이 여러 개의 스텝을 통해 이루어지기 때문에 일반적으로 GAN-based Model보다 샘플링하는 데 코스트가 크다는 단점이 있어 개선해야 할 부분도 있습니다.
본 논문은 기존 SMLD 방법론과 DDPM 방법론을 SDE 관점에서 설명하면서 Score-based Generative Model을 설명하는 일반적 프레임워크를 제공하는 데에 큰 의미가 있긴 하지만, 한편으론 SDE의 장점 중 하나인 Continuous Time variable을 극대화해 활용하거나, discretization을 일반화한 continuous diffusion process에 대한 분석 실험은 다소 부족하다고 할 수 있을 것 같습니다.
그럼에도 불구하고 아직 Score-based Generative model에 대한 연구 가능성이 많이 남아있는 만큼, 앞으로 많은 관심을 기울이셔도 좋을 것 같습니다.
* 잘못된 설명이 있거나 피드백이 필요해보이는 경우 댓글을 남겨주신다면 언제나 환영합니다. :)
[1] Hyvärinen, A. and Dayan, P., 2005. Estimation of non-normalized statistical models by score matching. Journal of Machine Learning Research, 6(4).
[2] Vincent, P., 2011. A connection between score matching and denoising autoencoders. Neural computation, 23(7), pp.1661-1674.
[3] Ho, J., Jain, A. and Abbeel, P., 2020. Denoising diffusion probabilistic models. arXiv preprint arXiv:2006.11239.
[4] Welling, M. and Teh, Y.W., 2011. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 681-688).
[##이학진##]
'Review' 카테고리의 다른 글
| Brief Review on Anchor-Free Object Detection (2019-2020) (3) | 2022.01.03 |
|---|---|
| 시간에 따른 도시 개발을 추적해봅시다 - SpaceNet 7 수상자 기술 분석 (0) | 2021.06.03 |
| 라벨 스무딩(Label smoothing), When Does Label Smoothing Help? (2) | 2020.07.15 |
| Real-world Super-resolution via Kernel Estimation and Noise Injection (0) | 2020.07.15 |
| Anomaly detection using one class neural networks (Raghavendra Chalapath, 2018) (1) | 2020.07.03 |




